

The formulation presented above only applies to stationary processes (i.e., time invariant). In the continuous case for the power spectral density, a cosine transform has been used as autocorrelation functions are even functions. In the discrete case, x(t) has been written as a function of the sample number n. This formulation takes advantage of the Weiner-Khinchin theorem, which states that the autocorrelation function of x(t) and the power spectral density are Fourier transform pairs. Power spectral density in terms of autocorrelation For any time series, the series’ autocorrelation function can be used to calculate the power spectral density: Here, the lower integration limit starts at t = 0 in order to account for causal signal behavior. Also for the discrete case, the time-domain signal x(t) contains N samples, and n refers to the sample number (total sampling time of T = NΔt). For the discrete case, the power spectral density can be calculated using the FFT algorithm. Here, the power spectral density is just the Fourier transform of the signal. Power spectral density for continuous and discrete signals The power spectral density S for a continuous or discrete signal in the time-domain x(t) is: Power Spectral Density: Continuous and Discrete SignalsĬontinuous and discrete signals are treated differently in terms of the mathematics, although the mathematical manipulations in continuous or discrete time are analogous. Here, the units of V2/Hz for the power spectral density represent the variance in the time-domain voltage level, which just happens to be proportional to the electrical power content for a given signal in the frequency domain. If you examine noise spectral bandwidth specifications for many components, you’ll see that the units are in V/√Hz, or in terms of the standard deviation in the signal level. Note that the use of a square unit in electronics is quite important as electrical power is proportional to V2 or I2. Power spectral densities in electronics may be written in W/Hz or dBm/Hz. If the units of your time-domain signal are V, then the units of power spectral density are V2/Hz, and the units for the bandlimited power spectrum are V2. This is likely the primary source of confusion around the terms “power spectrum” and “power spectral density.” For a given power spectral density S, the bandlimited power spectrum is:īandlimited power spectrum vs. This quantity is sometimes called a bandlimited power spectrum, or simply power spectrum. power spectral density arises when we consider the total signal content within a limited band. One important distinction between power spectrum vs. Calculating the Bandlimited Power Spectrum Measurements are always gathered in the time domain, after which they can be converted to the frequency domain for further analysis. Such a signal could be a broadband noise measurement, a harmonic analog signal, or a wideband signal of any type. Power spectrum and power spectral density are agnostic to the type of signal that is used to generate an intensity distribution in the frequency domain. In other words, these two terms are related to some other important concepts in signal processing, and it helps to understand the fundamental measurements that go into creating a power spectrum. The two terms are sometimes distinguished by the time-domain input that was used to generate the frequency-domain distribution.
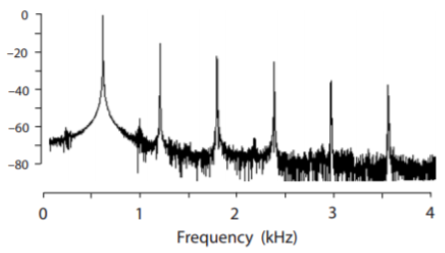
The two terms both describe how the intensity of a time-varying signal is distributed in the frequency domain.

These two terms are used interchangeably throughout the signal processing and mathematics communities at a conceptual level, there is no difference between these two terms. This is often used interchangeably with power spectrum, but there is no difference between power spectrum vs. The principle mathematical tool in your toolbox is an FFT and power spectral density, which shows you how the signal level is distributed across the frequency domain. Your equalizer bars are really showing you the intensity of sound within a specific bandwidth.Īlthough converting an electrical signal level into LED light on an equalizer bar is rather simple, there are more elegant ways to examine signal intensity in different frequency ranges. As a child, I used to wonder what they meant, and with some experimentation I realized they said something about the sound level for different pitches. Those green and red equalizer bars on console stereo systems? They show you some important information about audio signals.


 0 kommentar(er)
0 kommentar(er)
